Note
Click here to download the full example code or to run this example in your browser via Binder
Tuning a scikit-learn estimator with skopt¶
Gilles Louppe, July 2016 Katie Malone, August 2016 Reformatted by Holger Nahrstaedt 2020
If you are looking for a sklearn.model_selection.GridSearchCV replacement checkout
Scikit-learn hyperparameter search wrapper instead.
Problem statement¶
Tuning the hyper-parameters of a machine learning model is often carried out
using an exhaustive exploration of (a subset of) the space all hyper-parameter
configurations (e.g., using sklearn.model_selection.GridSearchCV), which
often results in a very time consuming operation.
In this notebook, we illustrate how to couple gp_minimize with sklearn’s
estimators to tune hyper-parameters using sequential model-based optimisation,
hopefully resulting in equivalent or better solutions, but within less
evaluations.
Note: scikit-optimize provides a dedicated interface for estimator tuning via
BayesSearchCV class which has a similar interface to those of
sklearn.model_selection.GridSearchCV. This class uses functions of skopt to perform hyperparameter
search efficiently. For example usage of this class, see
Scikit-learn hyperparameter search wrapper
example notebook.
print(__doc__)
import numpy as np
Objective¶
To tune the hyper-parameters of our model we need to define a model, decide which parameters to optimize, and define the objective function we want to minimize.
from sklearn.datasets import load_boston
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import cross_val_score
boston = load_boston()
X, y = boston.data, boston.target
n_features = X.shape[1]
# gradient boosted trees tend to do well on problems like this
reg = GradientBoostingRegressor(n_estimators=50, random_state=0)
Next, we need to define the bounds of the dimensions of the search space we want to explore and pick the objective. In this case the cross-validation mean absolute error of a gradient boosting regressor over the Boston dataset, as a function of its hyper-parameters.
from skopt.space import Real, Integer
from skopt.utils import use_named_args
# The list of hyper-parameters we want to optimize. For each one we define the
# bounds, the corresponding scikit-learn parameter name, as well as how to
# sample values from that dimension (`'log-uniform'` for the learning rate)
space = [Integer(1, 5, name='max_depth'),
Real(10**-5, 10**0, "log-uniform", name='learning_rate'),
Integer(1, n_features, name='max_features'),
Integer(2, 100, name='min_samples_split'),
Integer(1, 100, name='min_samples_leaf')]
# this decorator allows your objective function to receive a the parameters as
# keyword arguments. This is particularly convenient when you want to set
# scikit-learn estimator parameters
@use_named_args(space)
def objective(**params):
reg.set_params(**params)
return -np.mean(cross_val_score(reg, X, y, cv=5, n_jobs=-1,
scoring="neg_mean_absolute_error"))
Optimize all the things!¶
With these two pieces, we are now ready for sequential model-based optimisation. Here we use gaussian process-based optimisation.
from skopt import gp_minimize
res_gp = gp_minimize(objective, space, n_calls=50, random_state=0)
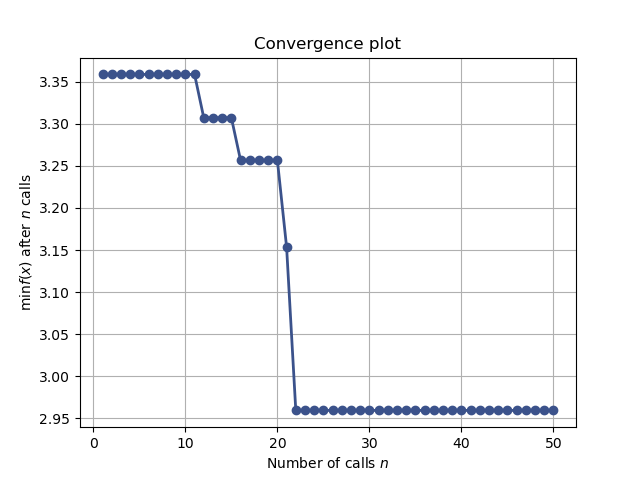
"Best score=%.4f" % res_gp.fun
Out:
'Best score=2.9593'
print("""Best parameters:
- max_depth=%d
- learning_rate=%.6f
- max_features=%d
- min_samples_split=%d
- min_samples_leaf=%d""" % (res_gp.x[0], res_gp.x[1],
res_gp.x[2], res_gp.x[3],
res_gp.x[4]))
Out:
Best parameters:
- max_depth=5
- learning_rate=0.112019
- max_features=13
- min_samples_split=51
- min_samples_leaf=1
Convergence plot¶
from skopt.plots import plot_convergence
plot_convergence(res_gp)
Out:
<AxesSubplot:title={'center':'Convergence plot'}, xlabel='Number of calls $n$', ylabel='$\\min f(x)$ after $n$ calls'>
Total running time of the script: ( 0 minutes 29.253 seconds)
Estimated memory usage: 32 MB

