Note
Click here to download the full example code or to run this example in your browser via Binder
Partial Dependence Plots 2D¶
Hvass-Labs Dec 2017 Holger Nahrstaedt 2020
Simple example to show the new 2D plots.
print(__doc__)
import numpy as np
from math import exp
from skopt import gp_minimize
from skopt.space import Real, Categorical, Integer
from skopt.plots import plot_histogram, plot_objective_2D, plot_objective
from skopt.utils import point_asdict
np.random.seed(123)
import matplotlib.pyplot as plt
dim_learning_rate = Real(name='learning_rate', low=1e-6, high=1e-2, prior='log-uniform')
dim_num_dense_layers = Integer(name='num_dense_layers', low=1, high=5)
dim_num_dense_nodes = Integer(name='num_dense_nodes', low=5, high=512)
dim_activation = Categorical(name='activation', categories=['relu', 'sigmoid'])
dimensions = [dim_learning_rate,
dim_num_dense_layers,
dim_num_dense_nodes,
dim_activation]
default_parameters = [1e-4, 1, 64, 'relu']
def model_fitness(x):
learning_rate, num_dense_layers, num_dense_nodes, activation = x
fitness = ((exp(learning_rate) - 1.0) * 1000) ** 2 + \
(num_dense_layers) ** 2 + \
(num_dense_nodes/100) ** 2
fitness *= 1.0 + 0.1 * np.random.rand()
if activation == 'sigmoid':
fitness += 10
return fitness
print(model_fitness(x=default_parameters))
Out:
1.518471835296799
search_result = gp_minimize(func=model_fitness,
dimensions=dimensions,
n_calls=30,
x0=default_parameters,
random_state=123
)
print(search_result.x)
print(search_result.fun)
Out:
/home/circleci/project/skopt/optimizer/optimizer.py:449: UserWarning: The objective has been evaluated at this point before.
warnings.warn("The objective has been evaluated "
[2.406607949145479e-06, 1, 5, 'relu']
1.011739365350369
for fitness, x in sorted(zip(search_result.func_vals, search_result.x_iters)):
print(fitness, x)
Out:
1.011739365350369 [2.406607949145479e-06, 1, 5, 'relu']
1.0201137666064235 [4.929660807339443e-06, 1, 5, 'relu']
1.0208250173428226 [5.447896159161361e-06, 1, 5, 'relu']
1.021667763257975 [0.00011447853469986647, 1, 5, 'relu']
1.0253849350948743 [1.2295084426825876e-06, 1, 5, 'relu']
1.031945862522914 [1e-06, 1, 5, 'relu']
1.045158959314699 [9.979802817806713e-05, 1, 5, 'relu']
1.0488386019266633 [9.857360440196212e-05, 1, 5, 'relu']
1.0558125627691162 [4.826899981343177e-06, 1, 5, 'relu']
1.0657569002436644 [1.2050706757608924e-06, 1, 5, 'relu']
1.0660997595359294 [1e-06, 1, 5, 'relu']
1.0669132800820755 [0.00010264544424985244, 1, 5, 'relu']
1.074939934810268 [3.738444474272787e-06, 1, 5, 'relu']
1.0751293946137341 [1.6008248563299506e-06, 1, 5, 'relu']
1.0876960557672355 [6.1111279732333165e-06, 1, 5, 'relu']
1.1301683677267782 [0.00012803374761470866, 1, 19, 'relu']
1.169066325243615 [0.00010510628709568241, 1, 33, 'relu']
1.4602213686635033 [0.0001, 1, 64, 'relu']
4.1749227163735005 [0.0001122604146483655, 2, 5, 'relu']
14.337540595777632 [4.961649309025573e-06, 2, 44, 'sigmoid']
15.811122459303194 [5.768045960755954e-05, 1, 366, 'relu']
20.75714626376416 [4.6648726500116405e-05, 4, 195, 'relu']
20.83105097254721 [3.629134387669892e-06, 3, 323, 'relu']
25.045498550233685 [1.5528231282886148e-05, 3, 380, 'relu']
25.725698564025883 [0.0010034940899532338, 4, 264, 'relu']
31.67808942295837 [9.214584006695478e-05, 4, 213, 'sigmoid']
32.60979725349034 [0.0007109209001237586, 3, 355, 'sigmoid']
36.436844941374716 [9.52877578124997e-06, 4, 306, 'sigmoid']
108.24130894769868 [0.01, 1, 5, 'relu']
117.22558971730295 [0.008953258961145084, 4, 399, 'relu']
space = search_result.space
print(search_result.x_iters)
search_space = {name: space[name][1] for name in space.dimension_names}
print(point_asdict(search_space, default_parameters))
Out:
[[0.0001, 1, 64, 'relu'], [0.0007109209001237586, 3, 355, 'sigmoid'], [9.214584006695478e-05, 4, 213, 'sigmoid'], [3.629134387669892e-06, 3, 323, 'relu'], [9.52877578124997e-06, 4, 306, 'sigmoid'], [5.768045960755954e-05, 1, 366, 'relu'], [1.5528231282886148e-05, 3, 380, 'relu'], [4.6648726500116405e-05, 4, 195, 'relu'], [0.008953258961145084, 4, 399, 'relu'], [4.961649309025573e-06, 2, 44, 'sigmoid'], [0.0010034940899532338, 4, 264, 'relu'], [0.00010510628709568241, 1, 33, 'relu'], [0.00011447853469986647, 1, 5, 'relu'], [0.0001122604146483655, 2, 5, 'relu'], [0.00012803374761470866, 1, 19, 'relu'], [5.447896159161361e-06, 1, 5, 'relu'], [4.929660807339443e-06, 1, 5, 'relu'], [4.826899981343177e-06, 1, 5, 'relu'], [0.00010264544424985244, 1, 5, 'relu'], [1e-06, 1, 5, 'relu'], [6.1111279732333165e-06, 1, 5, 'relu'], [1.6008248563299506e-06, 1, 5, 'relu'], [0.01, 1, 5, 'relu'], [3.738444474272787e-06, 1, 5, 'relu'], [9.979802817806713e-05, 1, 5, 'relu'], [9.857360440196212e-05, 1, 5, 'relu'], [1.2295084426825876e-06, 1, 5, 'relu'], [1e-06, 1, 5, 'relu'], [1.2050706757608924e-06, 1, 5, 'relu'], [2.406607949145479e-06, 1, 5, 'relu']]
OrderedDict([('activation', 0.0001), ('learning_rate', 1), ('num_dense_layers', 64), ('num_dense_nodes', 'relu')])
print("Plotting now ...")
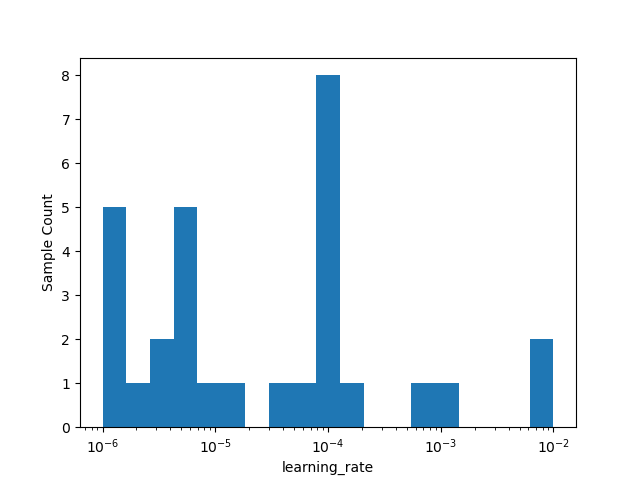
_ = plot_histogram(result=search_result, dimension_identifier='learning_rate',
bins=20)
plt.show()
Out:
Plotting now ...
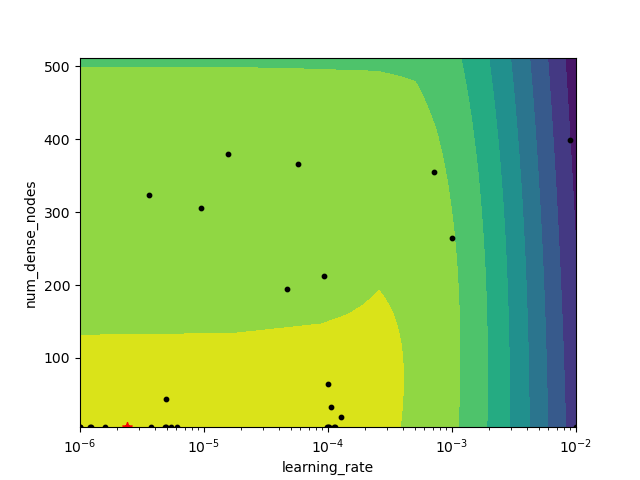
_ = plot_objective_2D(result=search_result,
dimension_identifier1='learning_rate',
dimension_identifier2='num_dense_nodes')
plt.show()
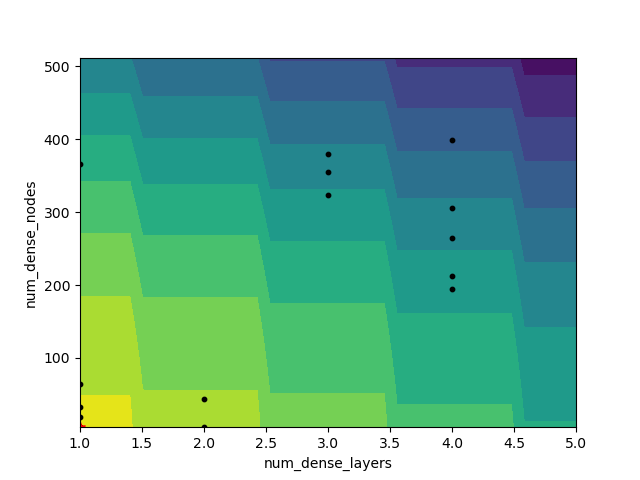
_ = plot_objective_2D(result=search_result,
dimension_identifier1='num_dense_layers',
dimension_identifier2='num_dense_nodes')
plt.show()
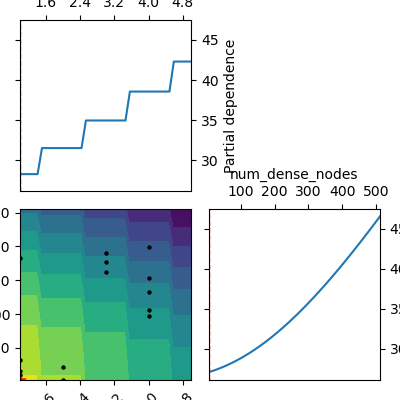
_ = plot_objective(result=search_result,
plot_dims=['num_dense_layers',
'num_dense_nodes'])
plt.show()
Total running time of the script: ( 0 minutes 11.861 seconds)
Estimated memory usage: 8 MB

