Getting started¶

Scikit-Optimize, or skopt, is a simple and efficient library to minimize (very) expensive and noisy black-box functions. It implements several methods for sequential model-based optimization. skopt aims to be accessible and easy to use in many contexts.

The library is built on top of NumPy, SciPy and Scikit-Learn.

We do not perform gradient-based optimization. For gradient-based optimization algorithms look at scipy.optimize here.

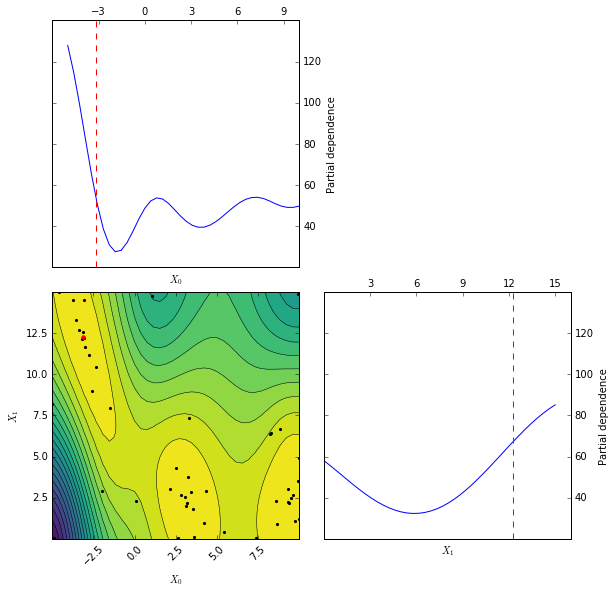
Approximated objective function after 50 iterations of gp_minimize. Plot made using plots.plot_objective.

Finding a minimum¶

Find the minimum of the noisy function f(x) over the range -2 < x < 2 with skopt:

>>> import numpy as np
>>> from skopt import gp_minimize
>>> np.random.seed(123)
>>> def f(x):
...     return (np.sin(5 * x[0]) * (1 - np.tanh(x[0] ** 2)) *
...             np.random.randn() * 0.1)
>>>
>>> res = gp_minimize(f, [(-2.0, 2.0)], n_calls=20)
>>> print("x*=%.2f f(x*)=%.2f" % (res.x[0], res.fun))
x*=0.85 f(x*)=-0.06

For more control over the optimization loop you can use the skopt.Optimizer class:

>>> from skopt import Optimizer
>>> opt = Optimizer([(-2.0, 2.0)])
>>>
>>> for i in range(20):
...     suggested = opt.ask()
...     y = f(suggested)
...     res = opt.tell(suggested, y)
>>> print("x*=%.2f f(x*)=%.2f" % (res.x[0], res.fun))
x*=0.27 f(x*)=-0.15

For more read our Bayesian optimization with skopt and the other examples.