Note

Click here to download the full example code or to run this example in your browser via Binder

Exploration vs exploitation¶

Sigurd Carlen, September 2019. Reformatted by Holger Nahrstaedt 2020

We can control how much the acqusition function favors exploration and exploitation by tweaking the two parameters kappa and xi. Higher values means more exploration and less exploitation and vice versa with low values.

kappa is only used if acq_func is set to “LCB”. xi is used when acq_func is “EI” or “PI”. By default the acqusition function is set to “gp_hedge” which chooses the best of these three. Therefore I recommend not using gp_hedge when tweaking exploration/exploitation, but instead choosing “LCB”, “EI” or “PI.

The way to pass kappa and xi to the optimizer is to use the named argument “acq_func_kwargs”. This is a dict of extra arguments for the aqcuisittion function.

If you want opt.ask() to give a new acquisition value imdediatly after tweaking kappa or xi call opt.update_next(). This ensures that the next value is updated with the new acquisition parameters.

print(__doc__)

import numpy as np
np.random.seed(1234)
import matplotlib.pyplot as plt

Toy example¶

First we define our objective like in the ask-and-tell example notebook and define a plotting function. We do however only use on initial random point. All points afterthe first one is therefore choosen by the acquisition function.

from skopt.learning import ExtraTreesRegressor
from skopt import Optimizer

noise_level = 0.1

# Our 1D toy problem, this is the function we are trying to
# minimize
def objective(x, noise_level=noise_level):
    return np.sin(5 * x[0]) * (1 - np.tanh(x[0] ** 2)) +\
           np.random.randn() * noise_level

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points = 1,
                acq_optimizer="sampling")

x = np.linspace(-2, 2, 400).reshape(-1, 1)
fx = np.array([objective(x_i, noise_level=0.0) for x_i in x])

from skopt.acquisition import gaussian_ei
def plot_optimizer(opt, x, fx):
    model = opt.models[-1]
    x_model = opt.space.transform(x.tolist())

    # Plot true function.
    plt.plot(x, fx, "r--", label="True (unknown)")
    plt.fill(np.concatenate([x, x[::-1]]),
             np.concatenate([fx - 1.9600 * noise_level,
                             fx[::-1] + 1.9600 * noise_level]),
             alpha=.2, fc="r", ec="None")

    # Plot Model(x) + contours
    y_pred, sigma = model.predict(x_model, return_std=True)
    plt.plot(x, y_pred, "g--", label=r"$\mu(x)$")
    plt.fill(np.concatenate([x, x[::-1]]),
             np.concatenate([y_pred - 1.9600 * sigma,
                             (y_pred + 1.9600 * sigma)[::-1]]),
             alpha=.2, fc="g", ec="None")

    # Plot sampled points
    plt.plot(opt.Xi, opt.yi,
             "r.", markersize=8, label="Observations")

    acq = gaussian_ei(x_model, model, y_opt=np.min(opt.yi))
    # shift down to make a better plot
    acq = 4 * acq - 2
    plt.plot(x, acq, "b", label="EI(x)")
    plt.fill_between(x.ravel(), -2.0, acq.ravel(), alpha=0.3, color='blue')

    # Adjust plot layout
    plt.grid()
    plt.legend(loc='best')

We run a an optimization loop with standard settings

for i in range(30):
    next_x = opt.ask()
    f_val = objective(next_x)
    opt.tell(next_x, f_val)
# The same output could be created with opt.run(objective, n_iter=30)
plot_optimizer(opt, x, fx)

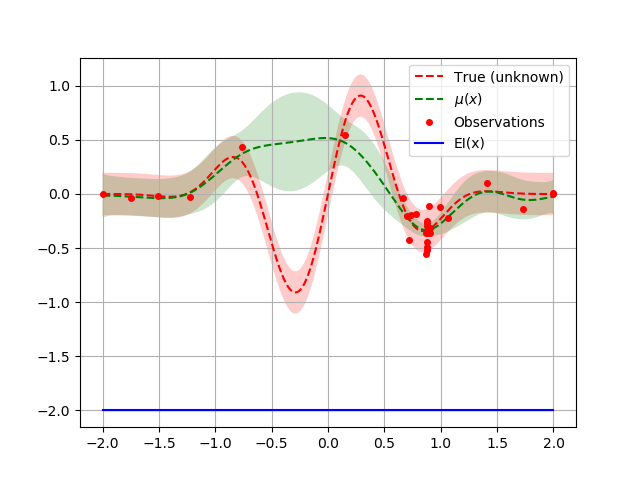
../_images/sphx_glr_exploration-vs-exploitation_001.png

We see that some minima is found and “exploited”

Now lets try to set kappa and xi using’to other values and pass it to the optimizer:

acq_func_kwargs = {"xi": 10000, "kappa": 10000}

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

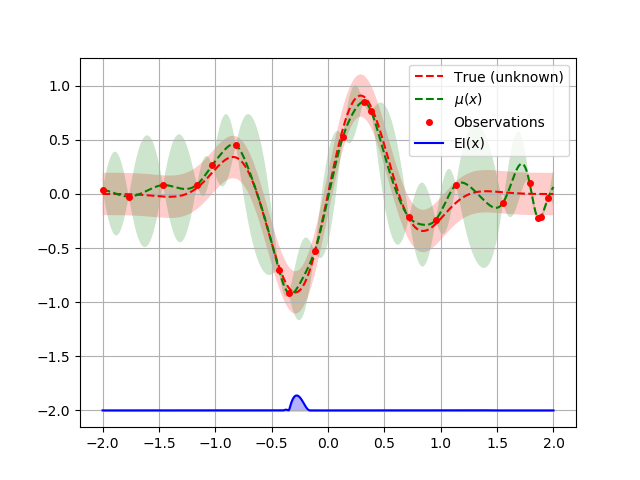
../_images/sphx_glr_exploration-vs-exploitation_002.png

We see that the points are more random now.

This works both for kappa when using acq_func=”LCB”:

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="LCB", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

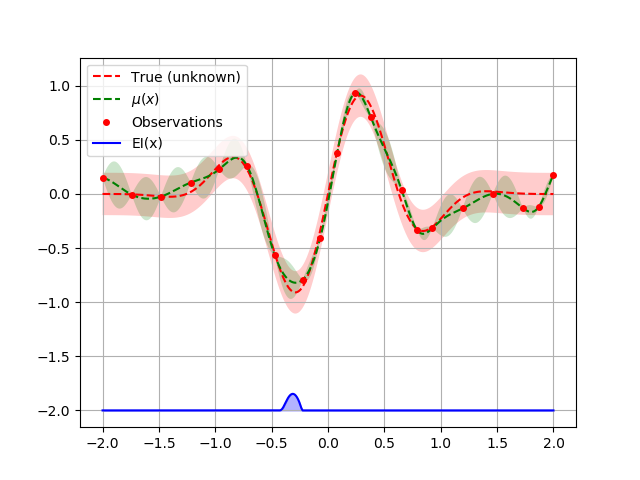
../_images/sphx_glr_exploration-vs-exploitation_003.png

And for xi when using acq_func=”EI”: or acq_func=”PI”:

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="PI", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

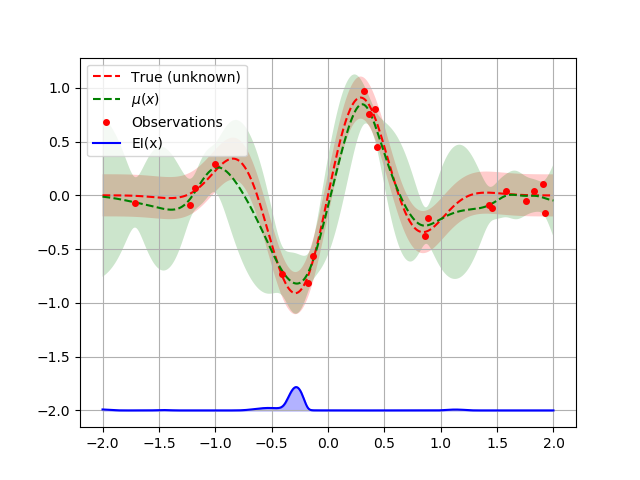
../_images/sphx_glr_exploration-vs-exploitation_004.png

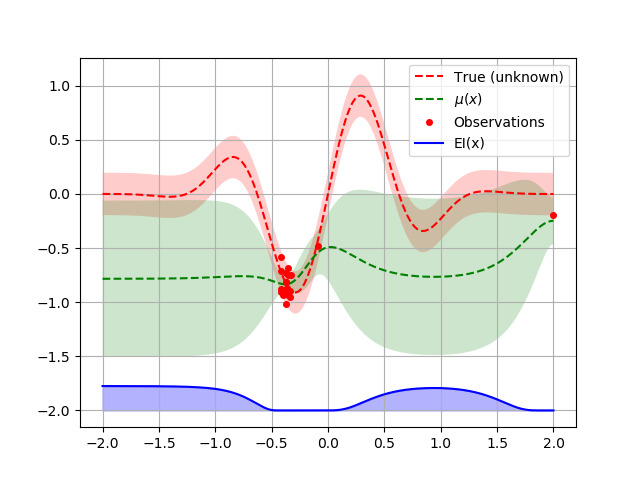
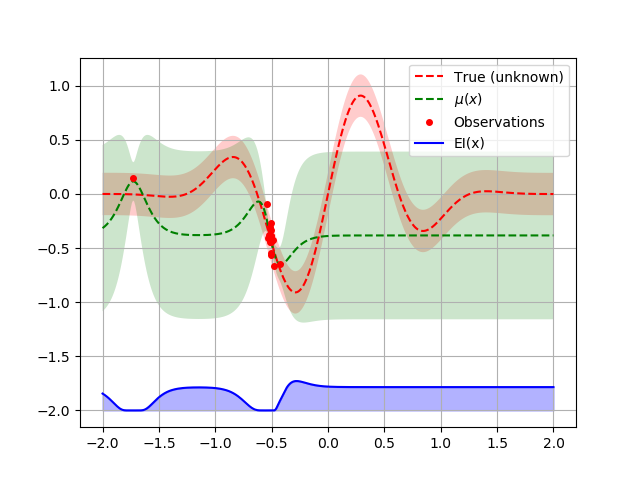
We can also favor exploitaton:

acq_func_kwargs = {"xi": 0.000001, "kappa": 0.001}

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="LCB", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

../_images/sphx_glr_exploration-vs-exploitation_005.png

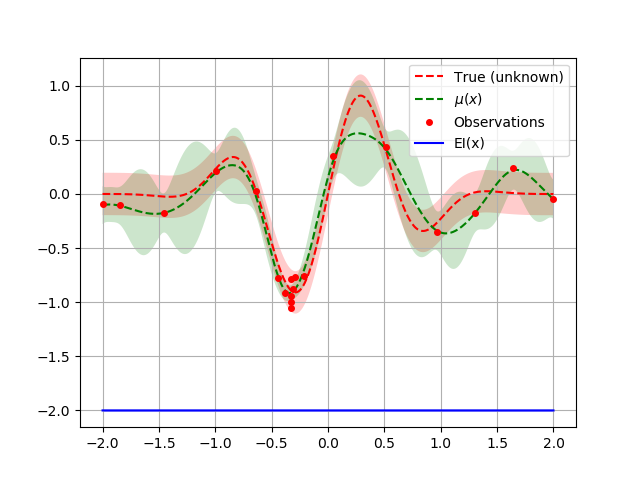
opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="EI", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

../_images/sphx_glr_exploration-vs-exploitation_006.png

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="PI", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

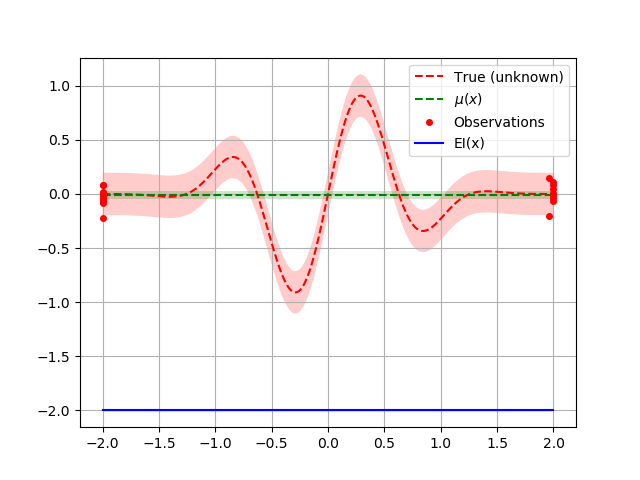
../_images/sphx_glr_exploration-vs-exploitation_007.png

Note that negative values does not work with the “PI”-acquisition function but works with “EI”:

acq_func_kwargs = {"xi": -1000000000000}

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="PI", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

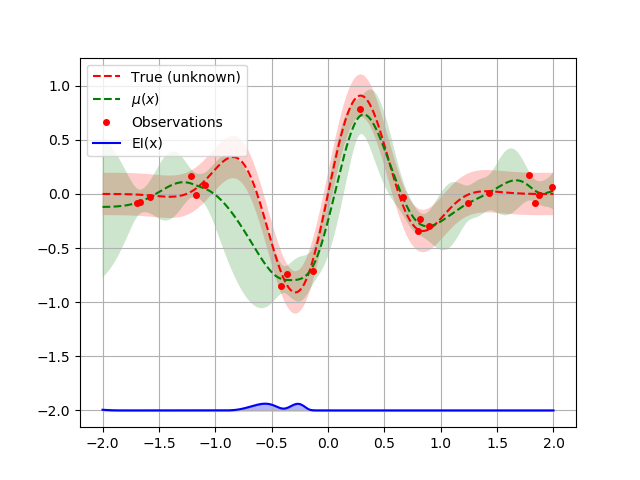
../_images/sphx_glr_exploration-vs-exploitation_008.png

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="EI", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

../_images/sphx_glr_exploration-vs-exploitation_009.png

Changing kappa and xi on the go¶

If we want to change kappa or ki at any point during our optimization process we just replace opt.acq_func_kwargs. Remember to call opt.update_next() after the change, in order for next point to be recalculated.

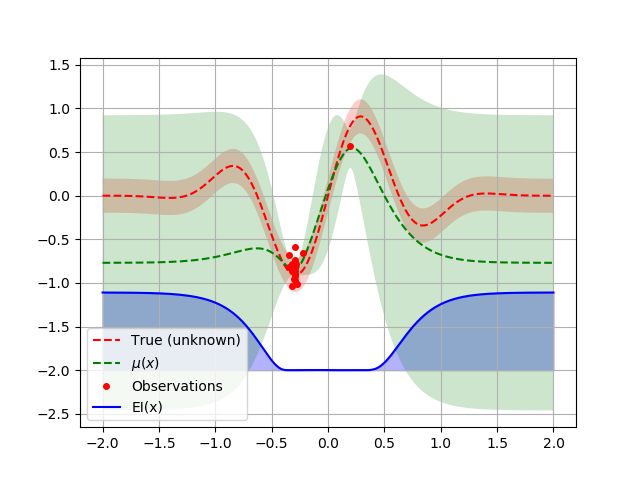
acq_func_kwargs = {"kappa": 0}

opt = Optimizer([(-2.0, 2.0)], "GP", n_initial_points=1,
                acq_func="LCB", acq_optimizer="sampling",
                acq_func_kwargs=acq_func_kwargs)

opt.acq_func_kwargs

Out:

{'kappa': 0}

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

../_images/sphx_glr_exploration-vs-exploitation_010.png

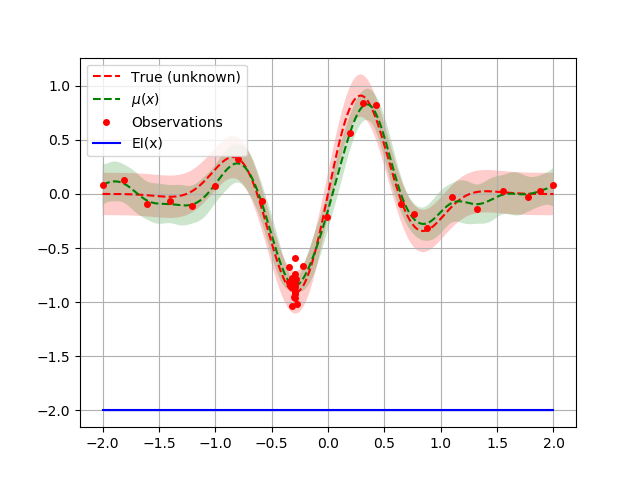
acq_func_kwargs = {"kappa": 100000}

opt.acq_func_kwargs = acq_func_kwargs
opt.update_next()

opt.run(objective, n_iter=20)
plot_optimizer(opt, x, fx)

../_images/sphx_glr_exploration-vs-exploitation_011.png

Total running time of the script: ( 0 minutes 34.924 seconds)

Estimated memory usage: 8 MB

Gallery generated by Sphinx-Gallery